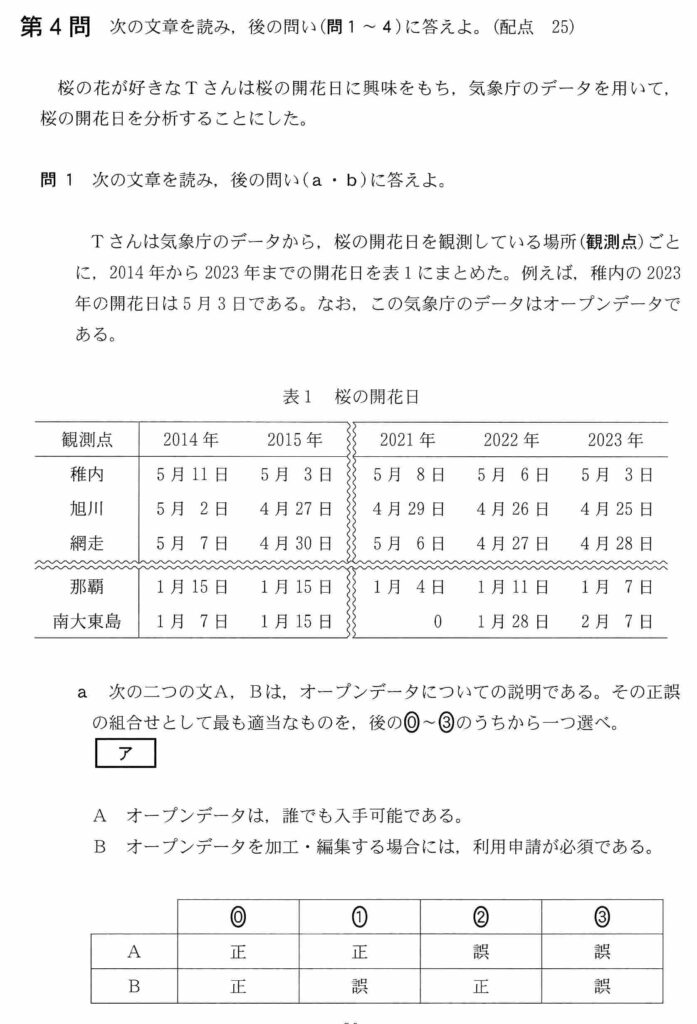
アはオープンデータについて単純に知識を問う問題。オープンデータは気象庁の過去の天気情報のように自由に誰でも入手できる(プレーンな)データで、加工編集は基本的に自由である。
ア:1

イの問題も知識を問う問題で、入力ミス・計測ミスなどで記録できなかったデータはどれかを問われている。
ウは「4月1日より早く開花した観測点の年ごとの変化」の可視化なので、3月末までに開花した観測点の数といえる。横軸が時間、縦軸が開花した観測点数となる。
イ:3
ウ:2


名古屋の実際の開花日は17日、400度開花推定日は2日遅い19日、600度開花推定日は1日早い16日なので、それぞれ開花差は②+2、⑤-1。
新潟と奈良の開花差は
400 600
新潟 4 -1
奈良 -1 -5 で、絶対値が小さいほど「近い」となる。
これを400、600それぞれに比較すると、「③新潟は600が近く、奈良は400が近い」となる。
エ:2
オ:5
カ:3
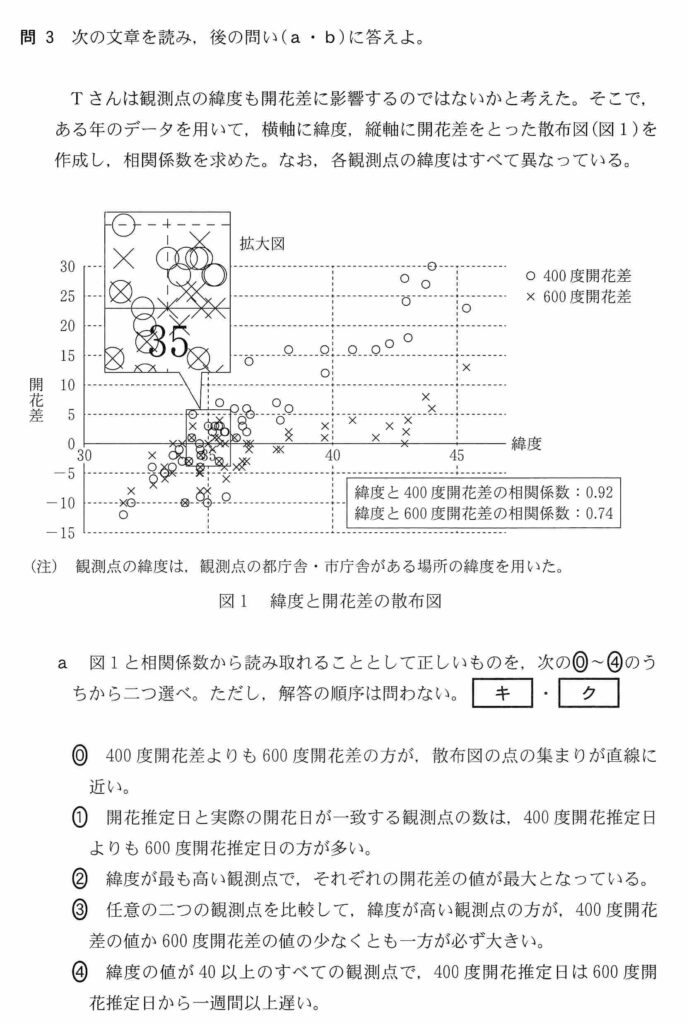
0:× 相関係数は400の方が高いため、600の方がばらついている
1:〇 開花差0のラインに載っているのは〇より×方が多い
2:× 緯度が2番目に高い観測点の方が開花差が離れている
3:× 全体的に右肩あがりな傾向にあるが、同じ緯度の観測点でどの×と〇がペアなのかが不確定なので、必ずといえない
4:〇 緯度40度以上の×と〇を比べると、一番近い間隔でも7日以上〇が遅い
キ:1
ク:4

ケについて、G2はプラス方向に6マイナス方向に12ということで、絶対値では12が最大の開花差の開きとなる。G1の中央値は16なので、これ以下に半数が含まれていることになる。12以上、16以下となると15が該当する。
コについては縦軸0上に〇があれば400と実際の一致ということが分かるので、図1のみで分かる。
サについては、図1だけでは0線上の〇がG1かG2か分からず(氷点下を観測した地点かどうかが分からず)、図2と組み合わせることでG2に0が含まれていることが分かる。
ケ: 2
コ: 0
サ: 3
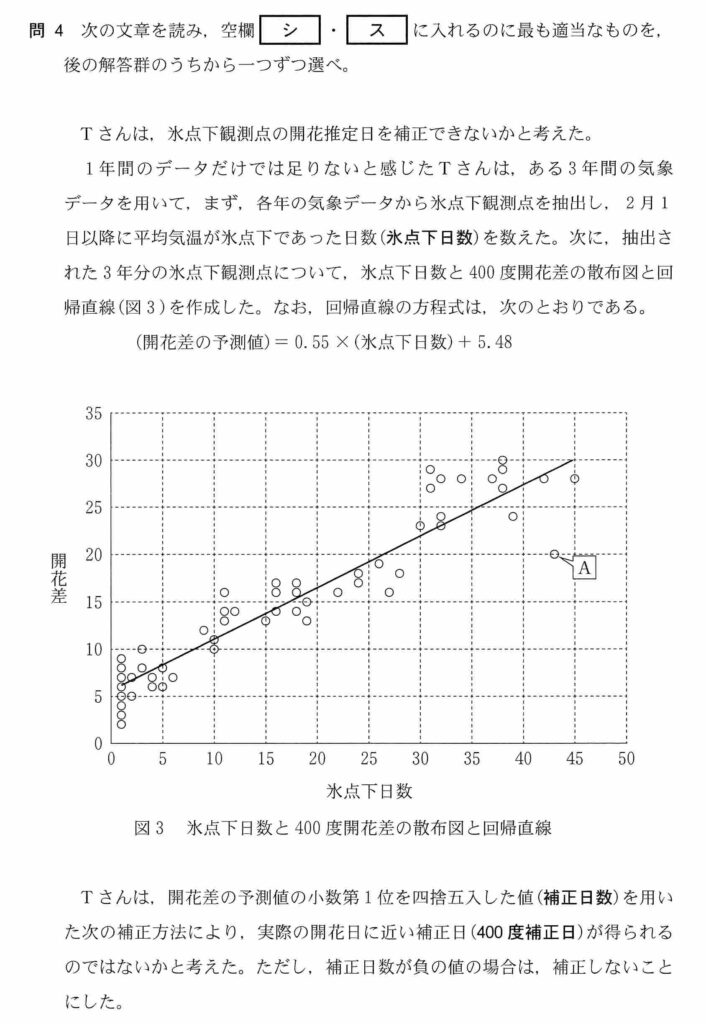

シについては一見すべて×に思える。
解答群②について、氷点下日数が1日の観測点は複数個所あり、この開花差は2~9である。氷点下日数が1日の開花差の予測値は、
0.55×1+5.48=6.03 で氷点下日数が1日の観測点は6日が補正日数となる。
400度開花推定日から補正日数をさかのぼった日を400度補正日として、この日数の方が(開花差に比べて)実際の開花日に近いと「うまく補正できる」とするため、この氷点下日数1日の観測箇所の400度補正日と開花差を比べると以下のようになる。
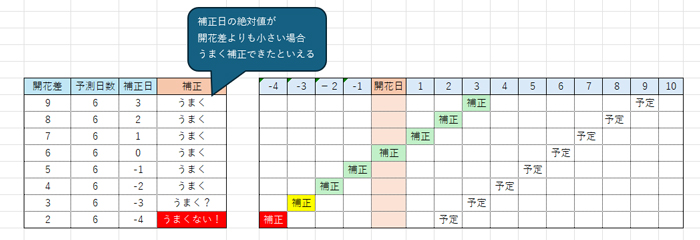
この中で、開花差3日だと開花差と補正日の絶対値が同じ(補正日の方が開花日に近くならない)、開花差2日では補正日が4日(補正日の方が遠い)になってこの2つが「うまく補正できない」となる。これに限られた試験時間の間に気が付けて確信をもって答えられる人は相当スゴイと思う。
①一見Aが外れ値っぽいので怪しく見えるが、氷点下日数43日、開花差20日の補正日は0.55×43+5.48 →29日で、開花差20日から29を引いた9日が400度補正日となるので、「うまく補正できている」となる。
③④について、これらは一見逆のことを言っているのでどちらかが該当すると思えそうになるが、氷点下日数が1日の8データに着目すると、回帰直線上または回帰直線より上(3データ)でも下(3データ)でも「うまく補正できている」のでどちらも間違いである。
スについては計算式に当てはめて計算するだけである。
観測点Xは推定日23日、氷点下日数18日。
0.55×18+5.48 →15日が補正日数となる。23日から15日を引くと4月8日が400度補正日となる。実際は12日が開花日で、その差は開花推定日が11日、補正日が4日であるため、観測点Xではうまく補正できたことになる。
シ:2
ス:1
実際に一度解いた問題を解きなおしながら解説を書いたが、大問3(プログラミング)、大問4(データサイエンス)については相当時間を割かれるため、試験時間内で解答するにはかなりのひらめき(複数の情報を同時に参照して関連の有無にきがつく)と判断力・決断力が必要になる。
ただ、初めての共通テストに取り入れられて難易度も分からずに解いた昨年に比べると、今年の問題は解きやすく解説もしやすいと感じている。おそらくこの1年間、予備校や教科書会社が設けた情報 I の共通テスト対策問題をたくさん解いていくことで、試験向きの考え方が身についたことによるものだと思える。
範囲は広いが、普段から特にプログラミングやデータサイエンスの問題に触れ、ただ解くだけでなく出題の意図も読み解きながら解法について馴染んでおくことが肝要だと感じられた。


コメントを残す